# 2.1 javaScript 内存管理
# 2.1.1 js 内存机制
# 🍅 内存空间:栈内存(stack)、堆内存(heap)
栈内存:所有原始数据类型都存储在栈内存中,如果删除一个栈原始数据,遵循先进后出;如下图:a 最先进栈,最后出栈。
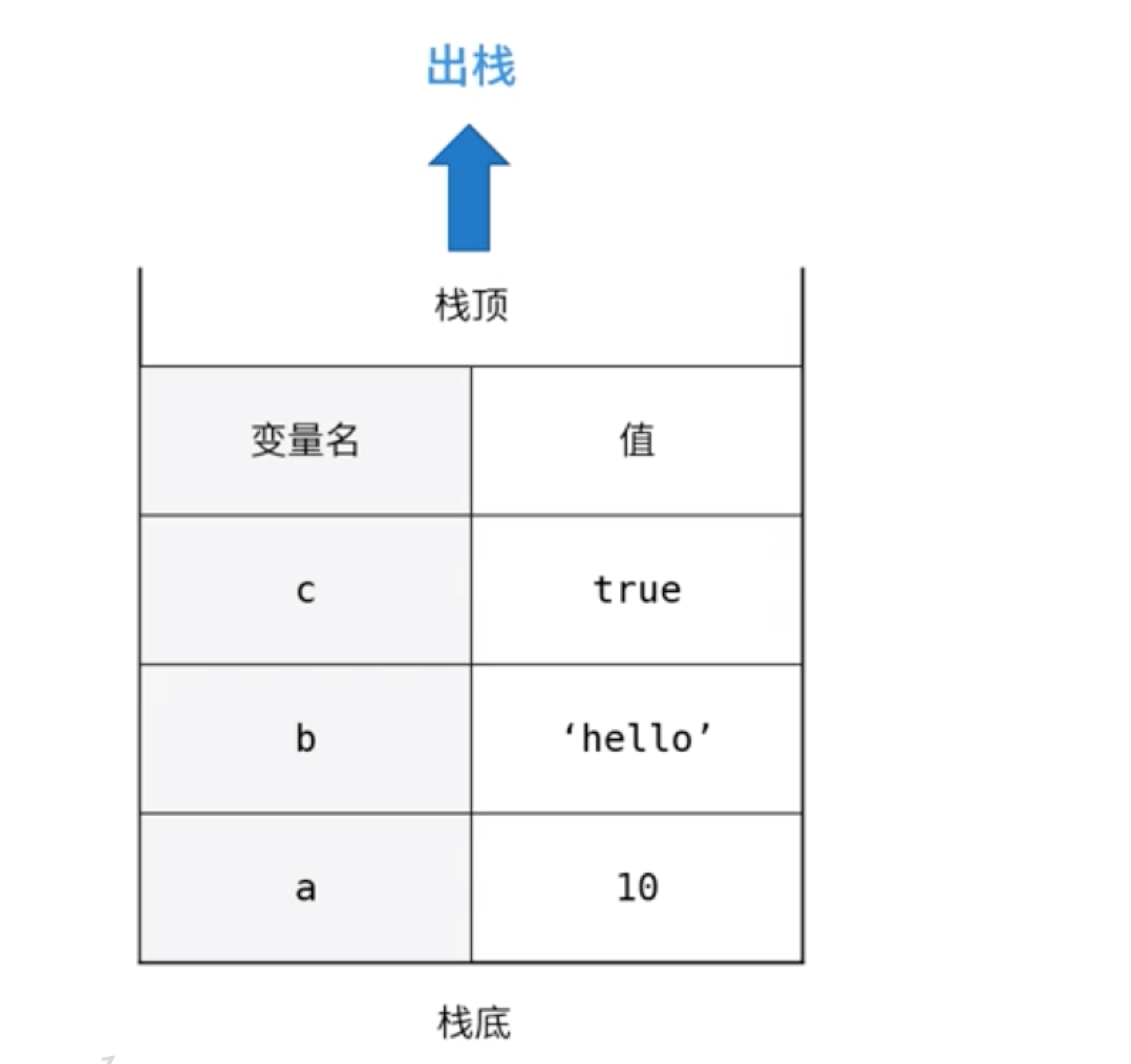
堆内存:引用数据类型会在堆内存中开辟一个空间,并且会有一个十六进制的内存地址,在栈内存中声明的变量的值就是十六进制的内存地址。
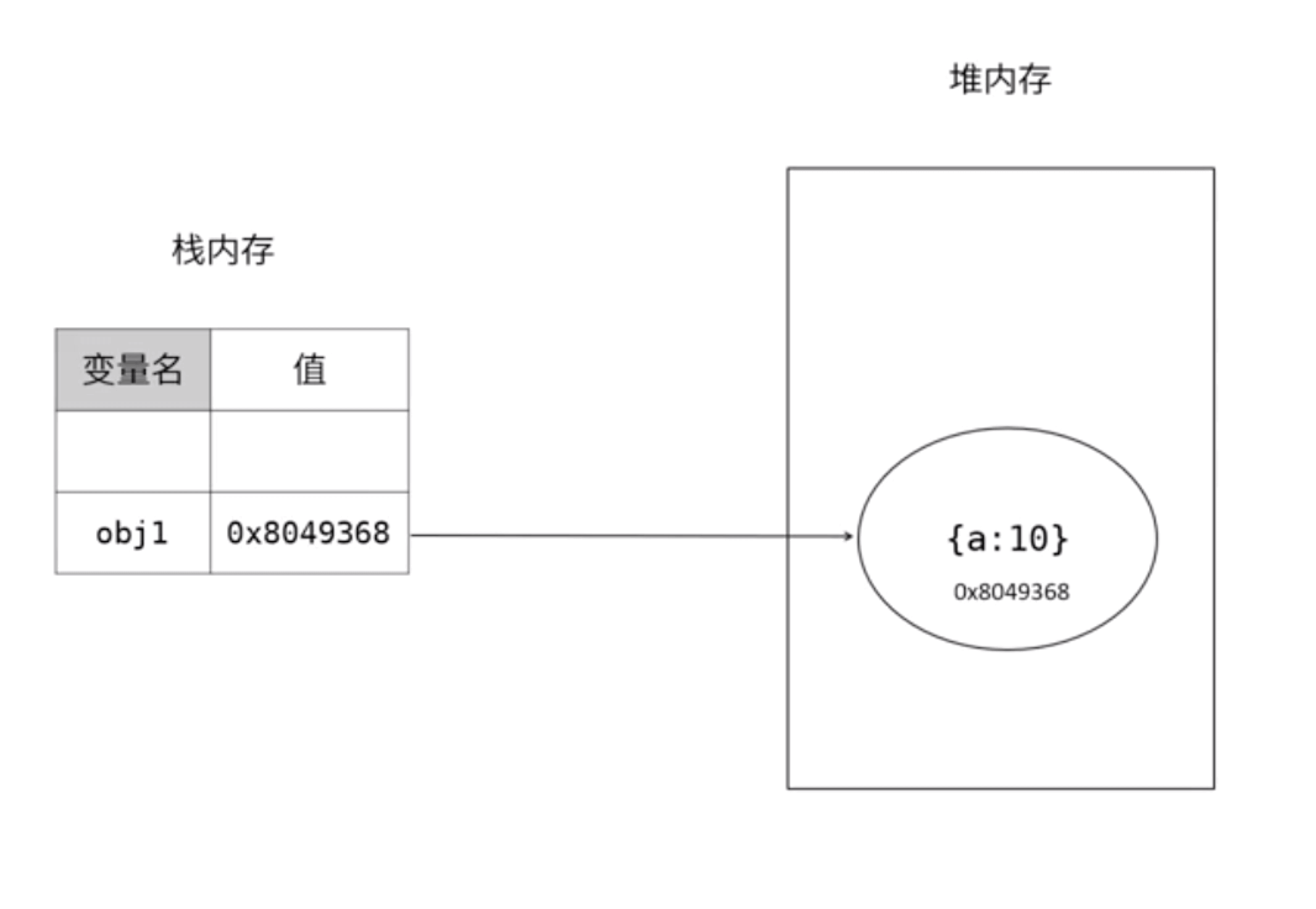
函数也是引用数据类型,我们定一个函数的时候,会在堆内存中开辟空间,会以字符串的形式存储到堆内存中去,如下图:
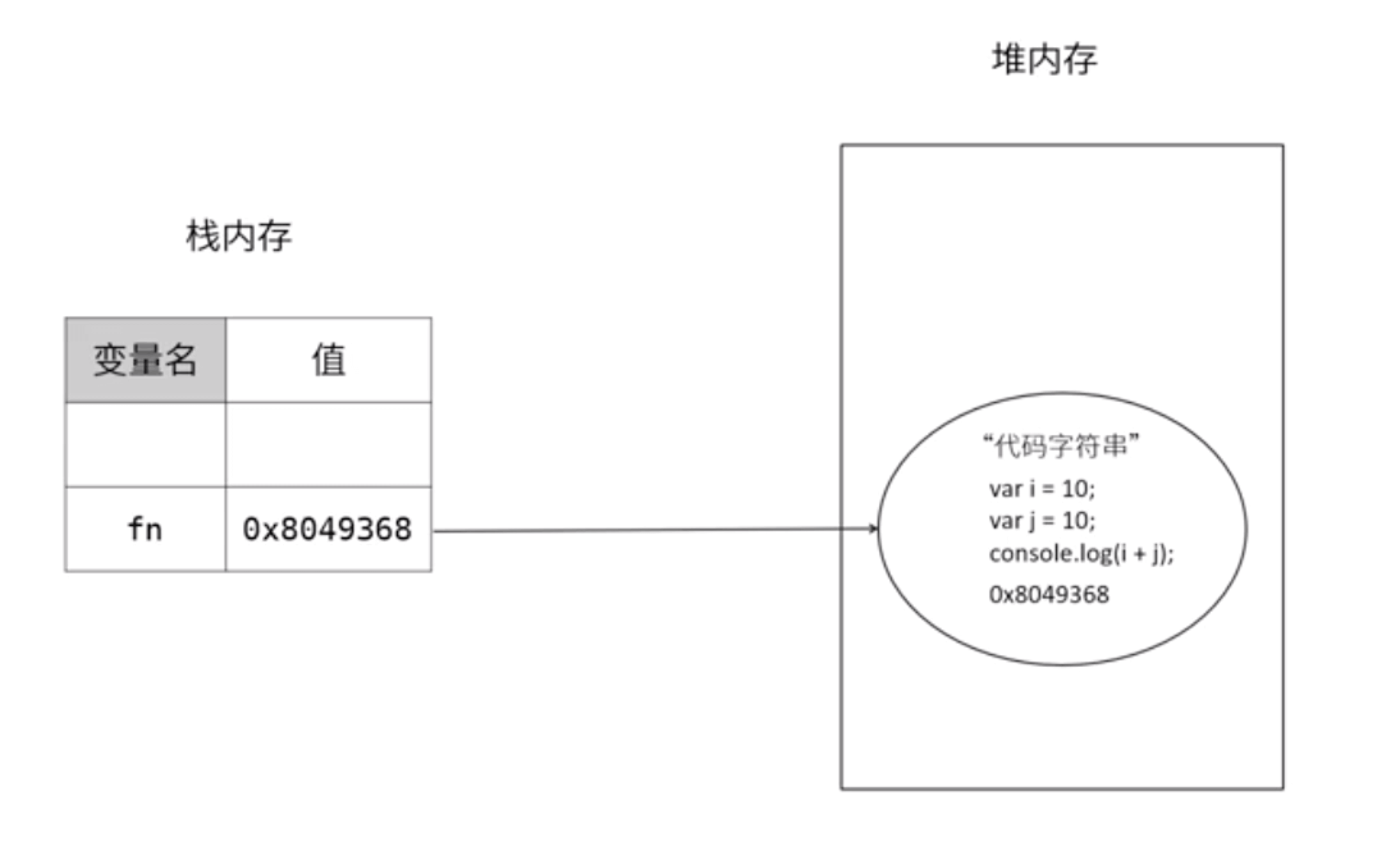
function fn() {
var i = 10
var j = 10
console.log(i + j)
}
// 我们直接打印fn会出现一段字符串
console.log(fn)
// 打印结果
/*
f fn() {
var i=10;
var j=10;
console.log(i+j)
}
*/
// 加上括号才执行里面的代码
fn() // 20
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# 2.1.2 垃圾回收
# 🍅 概念:(我们平时创建所有的数据类型都需要内存)
所谓的垃圾回收就是找出那些不再继续使用的变量,然后释放出其所占用的内存,垃圾回收会按照固定的时间间隔周期性的执行这一操作。
# 🍅 javaScript 使用的垃圾回收机制来自动管理内存,垃圾回收是把双刃剑;垃圾回收是不可见的
优势:可以大幅简化程序的内存管理代码,降低程序员的负担,减少因长时间运转而带来的内存泄漏问题。
不足:程序员无法掌控内存,javascript 没有暴露任何关于内存的 api,无法强迫进行垃圾回收,无法干预内存管理。
# 🍅 垃圾回收的方式
引用计数(reference counting)
跟踪记录每个值被引用的次数,如果一个值引用次数是 0,就表示这个值不再用到了,因此可以将这块内存释放
原理:每次引用加 1,被释放减 1,当这个值的引用次数变成 0 时,就将其内存空间释放。
let obj = { a: 10 } // 引用+1
let obj1 = { a: 10 } // 引用+1
obj = {} //引用减1
obj1 = null //引用为0
2
3
4
引用计数的 bug:循环引用
// ie8较早的浏览器,现在浏览器不会出现这个问题
function Fn() {
var objA = { a: 10 }
var objB = { b: 10 }
objA.c = objB
objB.c = objA
}
2
3
4
5
6
7
- 标记清除(现代浏览采用标记清除的方式)
# 🍅 概念:
标记清除指的是当变量进入环境时,这个变量标记为“进入环境”;而当变量离开环境时,则将其标记为“离开环境”,最后垃圾收集器完成内存清除工作,销毁那些带标记的值并回收它们所占用的内存空间(所谓的环境就是执行环境)
# 🍅 全局执行环境
- 最外围的执行环境
- 根据宿主环境的不同表示的执行环境的对象也不一样,在浏览器中全局执行环境被认为是 window 对象
- 全局变量和函数都是作为 window 对象的属性和方法创建的
- 某个执行环境中的所有代码执行完毕后,该环境被销毁,保存在其中的所有变量和函数定义也随之销毁(全局执行环境只有当关闭网页的时候才会被销毁)
# 🍅 环境栈(局部)
- 每个函数都有自己的执行环境,当执行流进入一个函数时,函数的环境就会被推入一个环境栈中。而在函数执行之后,栈将其环境弹出,把控制权返回给之前的执行环境,ECMAScript 程序中的执行流正是由这个方便的机制控制着
function foo (){
var a = 10 // 被标记进入执行环境
var b = ‘hello’ // 被标记进入执行环境
}
foo() //执行完毕,a 和 b 被标记离开执行环境,内存被回收
2
3
4
5
# 2.1.3 V8 内存管理机制
# 🍅 V8 引擎限制内存的原因
- V8 最初为浏览器设计,不太可能遇到大量内存的使用场景(表层原因)
- 防止因为垃圾回收所导致的线程暂停执行的时间过长(深层原因,按照官方的说法以 1.5G 的垃圾回收为例,v8 做一次小的垃圾回收需要 50 毫秒以上,做一次非增量的垃圾回收需要 1 秒以上,这里的时间是指 javascript 线程暂停执行的时间,这是不可接受的, v8 直接限制了内存的大小,如果说在 node.js 中操作大内存的对象,可以通过去修改设置去完成,或者是避开这种限制,1.7g 是在 v8 引擎方面做的限制,我们可以使用 buffer 对象,而 buffer 对象的内存分配是在 c++层面进行的,c++的内存不受 v8 的限制)
# 🍅 V8 回收策略
- v8 采用可一种分代回收的策略,将内存分为两个生代;新生代和老生代
- v8 分别对新生代和老生代使用不同的回收算法来提升垃圾回收效率
# 🍅 新生代垃圾回收
from 和 to 组成一个Semispace(半空间)当我们分配对象时,先在 from 对象中进行分配,当垃圾回收运行时先检查 from 中的对象,当obj2需要回收时将其留在 from 空间,而ob1分配到 to 空间,然后进行反转,将 from 空间和 to 空间进行互换,进行垃圾
回收时,将 to 空间的内存进行释放,简而言之 from 空间存放不被释放的对象,to 空间存放被释放的对象,当垃圾回收时将 to 空间的对象全部进行回收
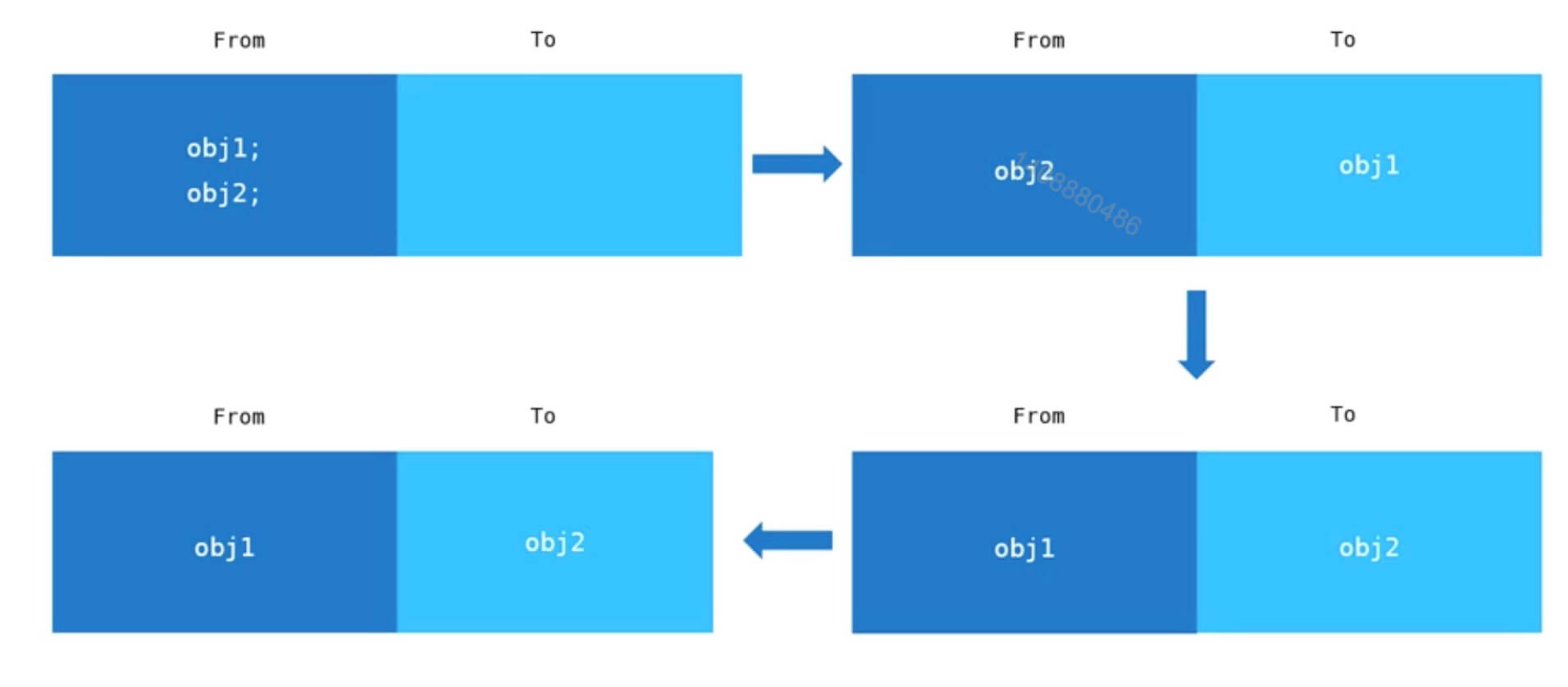
# 🍅 新生代对象的晋升(新生代中用来存放,生命较短的对象,老生代存放生命较长的对象)
- 在新生代垃圾回收的过程中,当一个对象经过多次复制后依然存活,它将会被认为是生命周期较长的对象,随后会被移动到老生代中,采取新的算法进行管理
- 在 From 空间和 To 空间进行反转的过程中,如果 To 空间中的使用量已经超过了 25%,那么就将 From 中的对象直接晋升到老生代内存空间中
# 🍅 老生代垃圾回收(有 2 种回收方法)
- 老生代内存空间是一个连续的结构

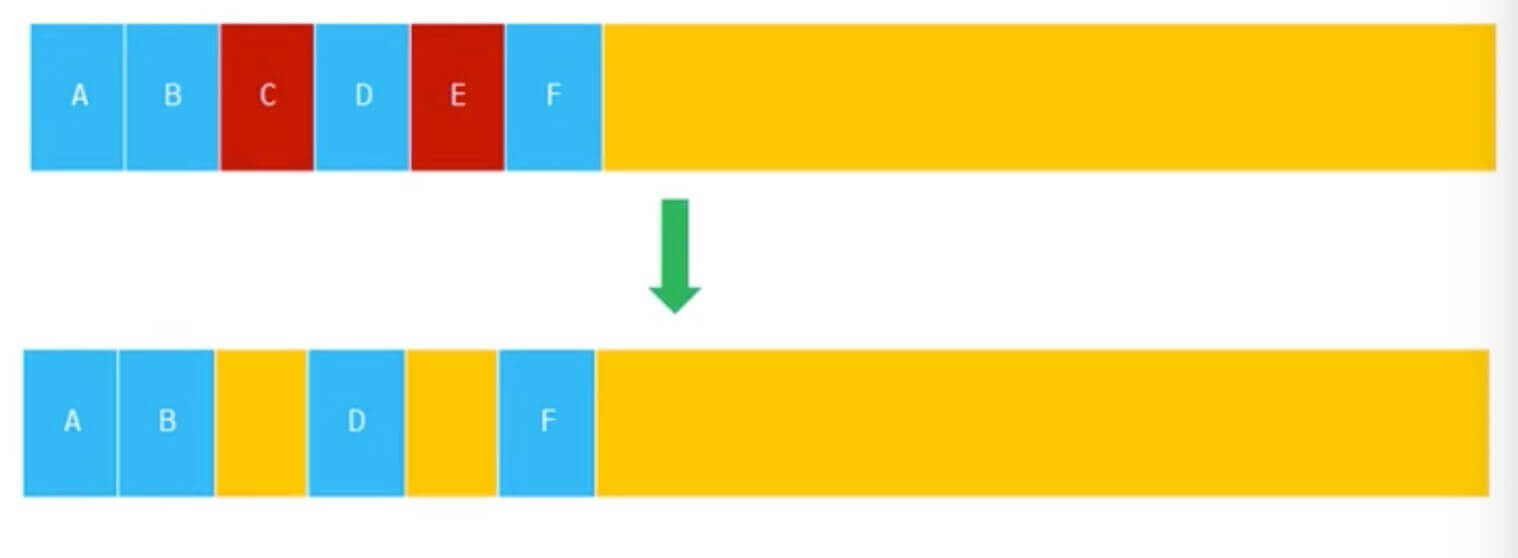
- 标记清除(Mark Sweep)
Mark Sweep 是将需要被回收的对象进行标记,在垃圾回收运行时直接释放相应的地址空间,红色的区域就是需要被回收的
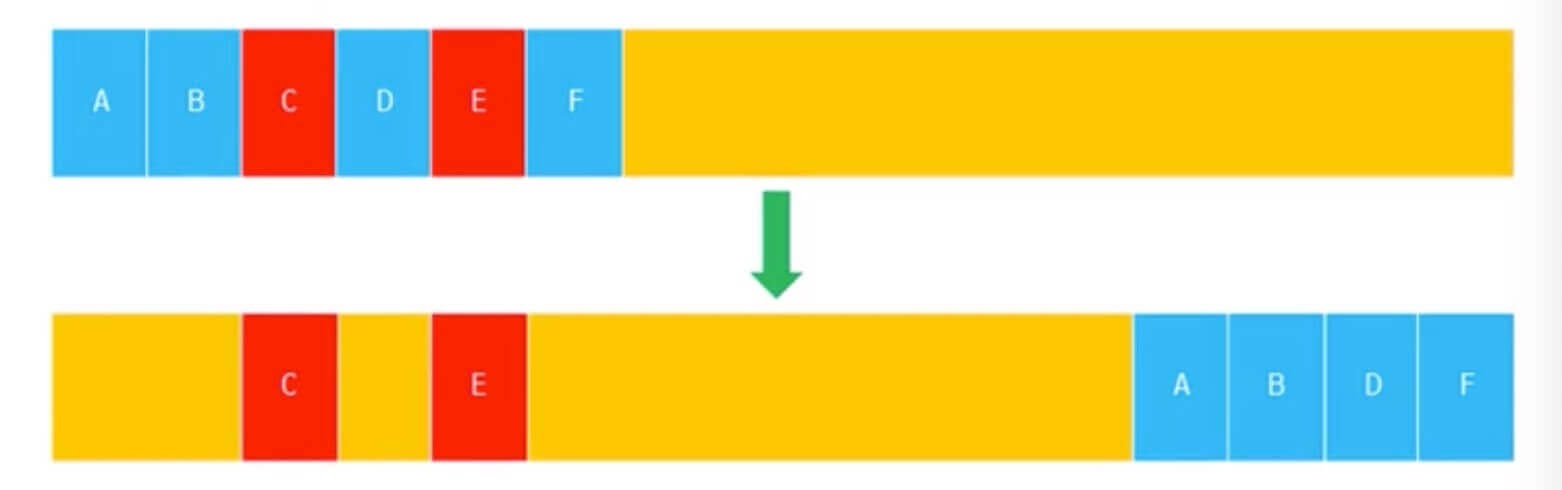
- 标记合并(Mark Compact)
Mark Compact 将存活的对象移动到一边,将需要被回收的对象移动到另一边,然后对需要被回收的对象区域进行整体的垃圾回收
# 2.2 如何保证你的代码质量
# 2.2.2 单元测试 (写一段代码去验证另一段代码,检测的对象可以是样式、功能、组件等)
# 🍅 概念
- 测试一种验证我们的代码是否可以按预期工作的方法
- 单元测试是对软件中的最小可测试单元进行检测和验证
# 🍅 前端单元测试的意义
- 检测出潜在的 bug
- 快速反馈功能输出,验证代码是否达到预期
- 保证代码重构的安全性
- 方便协作开发
# 🍅 单元测试代码
- 案例 1
let add = (a, b) => a + b //被测试的方法
let result = add(1, 2)
// 写的测试的代码
let expect = 4
if (result !== expect) {
throw new Error(`1+2应该等于${expect},但结果却是${result}`)
}
// 最后输出:Uncaught Error: 1+2应该等于4,但结果却是3
2
3
4
5
6
7
8
- 案例 2
//被测试的方法
let add = (a, b) => a + b
// 写的测试的代码
let expect = res => {
return {
toBe: actual => {
if (res !== actual) {
throw new Error(`预期值和实际值不符`)
}
}
}
}
// expect(add(1,2)).toBe(4)
let test = (desc, fn) => {
try {
fn()
console.log(`${desc}通过`)
} catch (err) {
console.log(`${desc}没有通过`)
}
}
test('加法测试', () => {
expect(add(1, 2)).toBe(3)
})
// 最后输出:加法测试通过
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
# 2.2.1 jest 的基础使用(facebook 的一套测试 javascript 的框架)
# 🍅 安装
- 安装 node
- yarn add -D jest
- 查看是否安装成功 npm ls jest
# 🍅 jest 的基础使用
- 创建一个文件夹,然后 npm init -y,然后下载 jest:yarn add -D jest
- 在文件夹下创建 math.js,这个文件是写被测试的代码;如下:
let add = (a, b) => a + b
module.exports = {
add
}
2
3
4
- 在文件夹下创建 math.test.js,这个文件写测试代码;如下。
const { add } = require('./math')
test('加法测试', () => {
expect(add(1, 2)).toBe(3)
})
2
3
4
- 配置 package.json 里的 script 脚本
"scripts": {
"test": "jest"
}
2
3
- 执行 npm test,测试成功会出现以下信息
PASS ./math.test.js
✓ 加法测试 (3ms)
Test Suites: 1 passed, 1 total
Tests: 1 passed, 1 total
Snapshots: 0 total
Time: 0.98s
Ran all test suites.
2
3
4
5
6
7
8
9
提示:具体代码可以在源码 examples/2.2/jest 目录下查看
# 2.3 提高代码的可靠性
# 2.3.1 函数式编程
含义:函数式编程是一种编程范式,是一种构建计算机程序结构和元素的风格,它把计算看作是对数据函数的评估,避免了状态的变化和数据的可变。
将我们的程序分解为一些更可复用,更可靠且更易于理解的部分,然后在将他们组合起来,形成一个更易推理的程序整体。
- 案例 1:对一个数组每项加+1
// 初级程序员
let arr = [1, 2, 3, 4]
let newArr = []
for (var i = 0; i < arr.length; i++) {
newArr.push(arr[i] + 1)
}
console.log(newArr) //[2, 3, 4, 5]
2
3
4
5
6
7
// 函数式编程
let arr = [1, 2, 3, 4]
let newArr = (arr, fn) => {
let res = []
for (var i = 0; i < arr.length; i++) {
res.push(fn(arr[i]))
}
return res
}
let add = item => item + 1 //每项加1
let multi = item => item * 5 //每项乘5
let sum = newArr(arr, add)
let product = newArr(arr, multi)
console.log(sum, product) // [2, 3, 4, 5] [5, 10, 15, 20]
2
3
4
5
6
7
8
9
10
11
12
13
14
# 2.3.2 纯函数
含义:如果函数的调用参数相同,则永远返回相同的结果。它不依赖于程序执行期间函数外部任何状态或数据的变化,必须只依赖于其输入的参数(相同的输入,必须得到相同的输出)。
// 纯函数
const calculatePrice=(price,discount)=> price * discount
let price = calculatePrice(200,0,8)
console.log(price)
2
3
4
// 不纯函数
const calculatePrice=(price,discount)=>{
const dt= new Date().toISOString()
console.log(`${dt}:${something}`)
return something
}
foo('hello')
2
3
4
5
6
7
# 2.3.3 函数副作用
当调用函数时,除了返回函数值外,还对注调用函数产生附加的影响
例如修改全局变量(函数外的变量)或修改参数
//函数外a被改变,这就是函数的副作用 let a = 5 let foo = () => (a = a * 10) foo() console.log(a) // 50 let arr = [1, 2, 3, 4, 5, 6] arr.slice(1, 3) //纯函数,返回[2,3],原数组不改变 arr.splice(1, 3) // 非纯函数,返回[2,3,4],原数组被改变 arr.pop() // 非纯函数,返回6,原数组改变1
2
3
4
5
6
7
8
9
10//通过依赖注入,对函数进行改进,所谓的依赖注入就是把不纯的部分作为参数传入,把不纯的代码提取出来;远离父函数;同时这么做不是为了消除副作用 //主要是为了控制不确定性 const foo = (d, log, something) => { const dt = d.toISOString() return log(`${dt}:${something}}`) } const something = '你好' const d = new Date() const log = console.log.bind(console) foo(d, log, something)1
2
3
4
5
6
7
8
9
10
11# 2.3.4 函数副作用可变性和不可变性
- 可变性是指一个变量创建以后可以任意修改
- 不可变性指一个变量,一旦被创建,就永远不会发生改变,不可变性是函数式编程的核心概念
// javascript中的对象都是引用类型,可变性使程序具有不确定性,调用函数foo后,我们的对象就发生了改变;这就是可变性,js中没有原生的不可变性 let data = { count: 1 } let foo = data => { data.count = 3 } console.log(data.count) // 1 foo(data) console.log(data.count) // 3 // 改进后使我们的数据具有不可变性 let data = { count: 1 } let foo = data => { let lily = JSON.parse(JSON.stringify(data)) // let lily= {...data} 使用扩展运算符去做拷贝,只能拷贝第一层 lily.count = 3 } console.log(data.count) // 1 foo(data) console.log(data.count) // 11
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# 2.4 compose 函数 pipe 函数
# 2.4.1 compose 函数
# 🍅 含义:
将需要嵌套执行的函数平铺
嵌套执行指的是一个函数的返回值将作为另一个函数的参数
# 🍅 作用:
实现函数式编程中的 Pointfree,使我们专注于转换而不是数据(Pointfree 不使用所有处理的值,只合成运算过程,即我们所指的无参数分割)
# 🍅 案例
计算一个数加 10 在乘以 10
// 一般会这么做
let calculate = x => (x+10) * 10
console.log(calculate(10))
2
3
4
// 用compose函数实现
let add = x => x + 10
let multiply = y => y * 10
console.log(multiply(add(10)))
let compose = function() {
let args = [].slice.call(arguments)
return function(x) {
return args.reduceRight(function(total, current) {
//从右往左执行args里的函数
console.log(total, current)
return current(total)
}, x)
}
}
let calculate = compose(multiply, add)
console.log(calculate, calculate(10)) // 200
// 用es6实现
const compose = (...args) => x => args.reduceRight((res, cb) => cb(res), x)
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
# 2.4.2 pipe 函数
pipe 函数 compose 类似,只不过从左往右执行
# 2.5 高阶函数
# 🍅 含义:
- 高阶函数是对其他函数进行操作的函数,可以将它们作为参数或返回它们
- 简单来说,高阶函数是一个函数,它接收函数作为参数或将函数作为输出返回
# 🍅 map/reduce/filter
// 用redece做累加
let arr = [1, 2, 3, 4, 5]
let sum = arr.reduce((pre, cur) => {
return pre + cur
}, 10)
// 用redece做去重
let arr = [1, 2, 3, 4, 5, 3, 3, 4]
let newArr = arr.reduce((pre, cur) => {
pre.indexOf(cur) === -1 && pre.push(cur)
return pre
}, [])
console.log(newArr) //[1, 2, 3, 4, 5]
2
3
4
5
6
7
8
9
10
11
12
13
# 🍅 flat
let arr = [[1, 2, 3, [23, 3, [1, 2]]]]
let arr1 = arr.flat(Infinity) // 多维转一维数组
let arr2 = arr.flat(2) // // 多维转二维数组,默认值是1
console.log(arr1, arr2) // [1, 2, 3, 23, 3, 1, 2] [1, 2, 3, 23, 3, Array(2)]
2
3
4
# 🍅 高阶函数的意义
- 参数为函数的高阶函数
// 参数为函数的高阶函数
function foo(f) {
// 判断是否为函数
if (typeof f === 'function') {
f()
}
}
foo(function() {})
2
3
4
5
6
7
8
- 返回值为函数的高阶函数
// 回值为函数的高阶函数
function foo (f){
rerutn function(){}
}
foo()
2
3
4
5
- 高阶函数的实际作用
let callback = value => {
console.log(value)
}
let foo = (value, fn) => {
if (typeof fn === 'function') {
fn(value)
}
}
foo('hello', callback)
2
3
4
5
6
7
8
9
# 2.6 常用函数
# 2.6.1 memozition(缓存函数)
含义:缓存函数是指将上次的计算结果缓存起来,当下次调用时,如果遇到相同的参数,就直接返回缓存中的数据
let add = (a, b) => a + b
// 假设memoize函数可以实现缓存
let calculate = memoize(add)
calculate(10, 20) // 30
calculate(10, 20) // 相同的参数,第二次调用是,从缓存中取出数据,而并非重新计算一次
2
3
4
5
# 🍅 实现原理:把参数和对应的结果数据存到一个对象中去,调用时,判断参数对应的数据是否存在,存在就返回对应的结果数据
// 缓存函数
let memoize = function(func) {
let cache = {}
return function(key) {
if (!cache[key] || (typeof cache[key] === 'number' && !!cache[key])) {
cache[key] = func.apply(this, arguments)
}
return cache[key]
}
}
2
3
4
5
6
7
8
9
10
/*
*hasher也是个函数,是为了计算key,如果传入了hasher,就用hasher函数计算key;
否则就用memoize函数传入的第一个参数,接着就去判断如果这个key没有被求值过,就去执行,
最后我们将这个对象返回
*/
var memoize = function(func, hasher) {
var memoize = function(key) {
var cache = memoize.cache
var address = '' + (hasher ? hasher.apply(this, arguments) : key)
if (!cache[address] || (typeof cache[key] === 'number' && !!cache[key])) {
cache[address] = func.apply(this, arguments)
}
return cache[address]
}
memoize.cache = {}
return memoize
}
// 缓存函数可以是fei bo
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# 🍅 案例:求斐波那且数列
// 不用memoize的情况下,会执行453次
var count = 0
var fibonacci = function(n) {
count++
return n < 2 ? n : fibonacci(n - 1) + fibonacci(n - 2)
}
for (var i = 0; i <= 10; i++) {
fibonacci(i) //453
}
console.log(count)
// 用memoize的情况下,会执行12次
var memoize = function(func, hasher) {
var memoize = function(key) {
var cache = memoize.cache
var address = '' + (hasher ? hasher.apply(this, arguments) : key)
if (!cache[address] || (typeof cache[key] === 'number' && !!cache[key])) {
cache[address] = func.apply(this, arguments)
}
return cache[address]
}
memoize.cache = {}
return memoize
}
fibonacci = memoize(fibonacci)
for (var i = 0; i <= 10; i++) {
fibonacci(i) //453 12
}
//缓存函数能应付大量重复计算,或者大量依赖之前的结果的运算场景
console.log(count)
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
# 2.6.2 curry(柯里化函数)
含义:在数学和计算机科学中,柯里化是一种将使用多个参数的一个函数转换成一些列使用一个参数的函数技术(把接受多个参数的函数转换成几个单一参数的函数)
// 没有柯里化的函数
function girl(name,age,single) {
return `${name}${age}${single}`
}
girl('张三',180,'单身')
// 柯里化的函数
function girl(name) {
return function (age){
return function (single){
return `${name}${age}${single}`
}
}
}
girl('张三')(180)('单身')
2
3
4
5
6
7
8
9
10
11
12
13
14
# 🍅 案例 1:检测字符串中是否有空格
// 封装函数去检测
let matching = (reg, str) => reg.test(str)
matching(/\s+/g, 'hello world') // true
matching(/\s+/g, 'abcdefg') // false
// 柯里化
let curry = reg => {
return str => {
return reg.test(str)
}
}
let hasSpace = curry(/\s+/g)
hasSpace('hello word') // true
hasSpace('abcdefg') // false
2
3
4
5
6
7
8
9
10
11
12
13
14
# 🍅 案例 2:获取数组对象中的 age 的属性值
let persons = [
{ name: 'zs', age: 21 },
{ name: 'ls', age: 22 }
]
// 不柯里化
let getage = persons.map(item => {
return item.age
})
// 用loadsh的curry 来实现
const _ = require('loadsh')
let getProp = _.curry((key, obj) => {
return obj[key]
})
person.map(getProp('age'))
2
3
4
5
6
7
8
9
10
11
12
13
14
# 🍅 柯里化这个概念实现本身就难,平时写代码很难用到,关键理解其思想
# 2.6.3 偏函数
# 🍅 比较:
柯里化是将一个多参数函数转换成多个单参数的函数,也就是将一个 n 元函数转换成 n 个一元函数
偏函数则固定一个函数的一个或多个参数,也就是将一个 n 元函数转换成一个 n-x 元的函数
柯里化:f(a,b,c)=f(a)(b)(c)
偏函数:f(a,b,c)=f(a,b)(c)
/*
用bind函数实现偏函数,bind的另一个用法使一个函数拥有预设的初始参数,将这些参数写在bind的第一个参数后,
当绑定函数调用时,会插入目标函数的初始位置,调用函数传入的参数会跟在bind传入的后面
*/
let add = (x, y) => x + y
let rst = add.bind(null, 1)
rst(2) //3
2
3
4
5
6
7
# 2.7 防抖和节流
# 🍅 为什么防抖和节流?
我们使用窗口的 resize,scorll,mousemove,mousehover;输入框等校验时,如果事件处理函数调用无限制,会加剧浏览器的负担,尤其是执行了操作 DOM 的函数,那不仅造成计算资源的浪费,还会降低程序运行速度,甚至造成浏览的奔溃,影响用户体验。
# 🍅 区别
- 防抖:就是触发多次事件,最后一次执行事件处理函数
- 节流:隔一段时间执行一次事件处理函数
# 2.7.1 函数防抖(debounce)
含义:当持续触发事件时,一定时间段内没有触发事件,事件处理函数才会执行一次,如果设定的时间到来之前,又一次触发了事件,就重新开始延时,‘函数防抖’的关键在于,在一个动作发生一定时间之后,才会执行特定的事件
# 🍅 案例:
<!DOCTYPE html>
<html lang="en">
<head>
<meta charset="UTF-8" />
<meta name="viewport" content="width=device-width, initial-scale=1.0" />
<meta http-equiv="X-UA-Compatible" content="ie=edge" />
<title>Document</title>
<style>
* {
margin: 0;
padding: 0;
}
#content {
width: 200px;
height: 200px;
line-height: 200px;
background-color: #ccc;
margin: 0 auto;
font-size: 60px;
text-align: center;
color: #000;
cursor: pointer;
}
</style>
</head>
<body>
<div id="content"></div>
<script>
/*
连续onmousemove在最后一次触发changeNum函数,
多余的处理函数的都会被clearTimeout掉
*/
let num=1
let oDiv= document.getElementById('content')
let changeNum=function () {
oDiv.innerHTML=num++
}
let deBounce = function (fn,delay){
let timer=null
return function (...args) {
if(timer) clearTimeout(timer)
timer = setTimeout(()=>{
fn(...args)
},delay)
}
}
oDiv.onmousemove=deBounce(changeNum,500)
// or
let _deBounce = deBounce(changeNum,500)
oDiv.onmousemove=function(){
_deBounce()
}
</script>
</body>
</html>
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
# 🍅 underscore 库 debounce 源码
_.debounce = function(func, wait, immediate) {
var timeout, result
var later = function(context, args) {
timeout = null
if (args) result = func.apply(context, args)
}
var debounced = restArguments(function(args) {
if (timeout) clearTimeout(timeout)
if (immediate) {
var callNow = !timeout
timeout = setTimeout(later, wait)
if (callNow) result = func.apply(this, args)
} else {
timeout = _.delay(later, wait, this, args)
}
return result
})
debounced.cancel = function() {
clearTimeout(timeout)
timeout = null
}
return debounced
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
# 2.7.2 函数节流(throttle)
含义:当持续触发事件时,保证一定时间段内只调用一次事件处理函数
# 🍅 案例:
<!DOCTYPE html>
<html lang="en">
<head>
<meta charset="UTF-8" />
<meta name="viewport" content="width=device-width, initial-scale=1.0" />
<meta http-equiv="X-UA-Compatible" content="ie=edge" />
<title>Document</title>
</head>
<body></body>
<button>点击</button>
<script>
/*
* 连续点击只会1000执行一次btnClick函数
*/
let obutton = document.getElementsByTagName('button')[0]
// 如果用箭头函数,箭头函数没有arguments,也不能通过apply改变this指向
function btnClick() {
console.log('我响应了')
}
/*
方法1: 定时器方式实现
缺点:第一次触发事件不会立即执行fn,需要等delay间隔过后才会执行
*/
let throttle = (fn, delay) => {
let flag = false
return function(...args) {
if (flag) return
flag = true
setTimeout(() => {
fn(...args)
flag = false
}, delay)
}
}
/*
方法2:时间戳方式实现
缺点:最后一次触发回调与前一次的触发回调的时间差小于delay,则最后一次触发事件不会执行回调
*/
let throttle = (fn, delay) => {
let _start = Date.now()
return function(...args) {
let _now = Date.now(),
that = this
if (_now - _start > delay) {
fn.apply(that, args)
start = Date.now()
}
}
}
// 方法3:时间戳与定时器结合
let throttle = (fn, delay) => {
let _start = Date.now()
return function(...args) {
let _now = Date.now(),
that = this,
remainTime = delay - (_now - _start)
if (remainTime <= 0) {
fn.apply(that, args)
} else {
setTimeout(() => {
fn.apply(that, args)
}, remainTime)
}
}
}
/*
方法4:requestAnimationFrame实现
优点:由系统决定回调函数的执行机制,60Hz的刷新频率,每次刷新都会执行一次回调函数,不
会引起丢帧和卡顿
缺点:1.有兼容性问题2.时间间隔有系统决定
*/
let throttle = (fn, delay) => {
let flag
return function(...args) {
if (!flag) {
requestAnimationFrame(function() {
fn.apply(that, args)
flag = false
})
}
flag = true
}
}
obutton.onclick = throttle(btnClick, 1000)
</script>
</html>
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
# 🍅 underscore 库 throttle 源码
_.throttle = function(func, wait, options) {
var timeout, context, args, result
var previous = 0
if (!options) options = {}
var later = function() {
previous = options.leading === false ? 0 : _.now()
timeout = null
result = func.apply(context, args)
if (!timeout) context = args = null
}
var throttled = function() {
var now = _.now()
if (!previous && options.leading === false) previous = now
var remaining = wait - (now - previous)
context = this
args = arguments
if (remaining <= 0 || remaining > wait) {
if (timeout) {
clearTimeout(timeout)
timeout = null
}
previous = now
result = func.apply(context, args)
if (!timeout) context = args = null
} else if (!timeout && options.trailing !== false) {
timeout = setTimeout(later, remaining)
}
return result
}
throttled.cancel = function() {
clearTimeout(timeout)
previous = 0
timeout = context = args = null
}
return throttled
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
# 2.7.3 防抖使用场景
<!DOCTYPE html>
<html lang="en">
<head>
<meta charset="UTF-8" />
<meta name="viewport" content="width=device-width, initial-scale=1.0" />
<meta http-equiv="X-UA-Compatible" content="ie=edge" />
<title>Document</title>
</head>
<body>
<input type="text" />
<!-- 防抖场景 -->
<script>
// 防抖函数
let deBounce = (fn, delay) => {
let timer = null
return function(...args) {
if (timer) clearTimeout(timer)
timer = setTimeout(() => {
fn(...args)
}, delay)
}
}
let oInput = document.getElementsByTagName('input')[0]
// 模拟请求
let ajax = message => {
let json = { message }
console.log(JSON.stringify(json))
}
let doAjax = deBounce(ajax, 200)
// 键盘弹起执行
oInput.addEventListener('keyup', e => {
doAjax(e.target.value)
})
</script>
</body>
</html>
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
# 2.8 深拷贝和浅拷贝
# 2.8.1 深拷贝&浅拷贝
对于原始数据类型,并没有深浅拷贝的区别,深浅拷贝都是对于引用数据类型而言,如果我们要赋值对象的所有属性都是引用类型可以用浅拷贝
# 🍅 浅拷贝:只复制一层对象,当对象的属性是引用类型时,实质复制的是其引用,当引用值发生改变时,也会跟着改变
# 🍅 深拷贝:深拷贝是另外申请了一块内存,内容和原来一样,更改原对象,拷贝对象不会发生改变
# 2.8.2 浅拷贝实现
# 🍅 for in 遍历实现
let shallCopy => obj=>{
let rst={}
for(let key in obj){
//只复制本身的属性(非继承过来的属性)枚举属性
if(obj.hasOwnProperty(key)){
rst[key]=obj[key]
}
}
return rst
}
let start ={
name:'古力娜扎',
age:'22',
friend:{
name:'邓超'
}
}
let copyStart=shallCopy(start)
copyStart.name="热巴"
copyStart.friend.name='黄渤'
// 拷贝的第一层层如果是引用类型,拷贝的其实是一个指针,所以拷贝对象改变会影响原对象
console.log(start.name,opyStart.friend.name) //古力娜扎 黄渤
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
# 🍅 Object.assign(target,source) (适用于对象)
可以把 n 个源对象拷贝到目标对象中去(拷贝的是可枚举属性)
let start = {
name: '古力娜扎',
age: '22',
friend: {
name: '邓超'
}
}
let returnedTarget = Object.assign({}, start)
2
3
4
5
6
7
8
# 🍅 扩展运算符...
let start = { name: '刘亦菲' }
let newStart = { ...start }
newStart.name = '迪丽热巴'
console.log(start.name) // 刘亦菲
2
3
4
# 🍅 slice(适用于数组)
let a = [1, 2, 3, 4]
let b = a.slice()
b[0] = 9
console.log(a) //[1,2,3,4]
2
3
4
# 2.8.3 深拷贝实现
# 🍅 JSON.parse(JSON.stringify(obj))
let obj = {
name: '小明',
dog: ['小花', '旺财']
}
let obj1 = JSON.parse(JSON.stringify(obj))
obj1.name = '小华'
obj1.dog[0] = '小白'
console.log(obj) // {name: "小明", dog: ['小花', '旺财']}
// 原数组并没有改变,说明实现了深拷贝
let richGirl = [
{
name: '开心',
car: ['宝马', '奔驰', '保时捷'],
deive: function() {},
age: undefined
}
]
let richBoy = JSON.parse(JSON.stringify(richGirl))
console.log(richBoy)
/*
1. 当属性值为undefined或函数,则序列化的结果会把函数或 undefined丢失
2. 对象中存在循环引用的情况也无法正确实现深拷贝
3. Symbol,不能被JSON序列化
4. RegExp、Error对象,JSON序列化的结果将只得到空对象
5. 会丢失对象原型
*/
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
# 🍅 递归实现深拷贝
let deepClone = obj => {
let newObj = Array.isArray(obj) ? [] : {}
if (obj && typeof obj === 'object') {
for (let key in obj) {
if (obj.hasOwnProperty(key)) {
if (obj[key] && typeof obj[key] === 'object') {
newObj[key] = deepClone(obj[key])
} else {
// 如果不是对象直接拷贝
newObj[key] = obj[key]
}
}
}
}
return newObj
}
let richGirl = {
name: '开心',
car: ['宝马', '奔驰', '保时捷'],
deive: function() {},
age: undefined
}
let richBoy = deepClone(richGirl)
richBoy.deive = '渣男开大G'
richBoy.name = '小明'
richBoy.car = ['哈罗单车', '膜拜']
richBoy.age = 20
console.log(richGirl)
console.log(richBoy)
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
# 2.8.4 第三方库实现拷贝
# 🍅 lodash
//cloneDeep: 深拷贝 clone:浅拷贝,此例子介绍深拷贝
const _ = require('lodash') //全部引入
const cloneDeep = require('lodash/cloneDeep') //引入单个方法,用的方法少建议用这种方式引入
let obj = {
name: '开心',
car: ['宝马', '奔驰', '保时捷'],
deive: function() {},
age: undefined
}
const newObj = cloneDeep(obj)
newObj.name = '不开心'
newObj.car[0] = '自行车'
console.log(obj, newObj) // 原对象不会改变
2
3
4
5
6
7
8
9
10
11
12
13

